抽象 (Abstraction)
计算机系统中的抽象
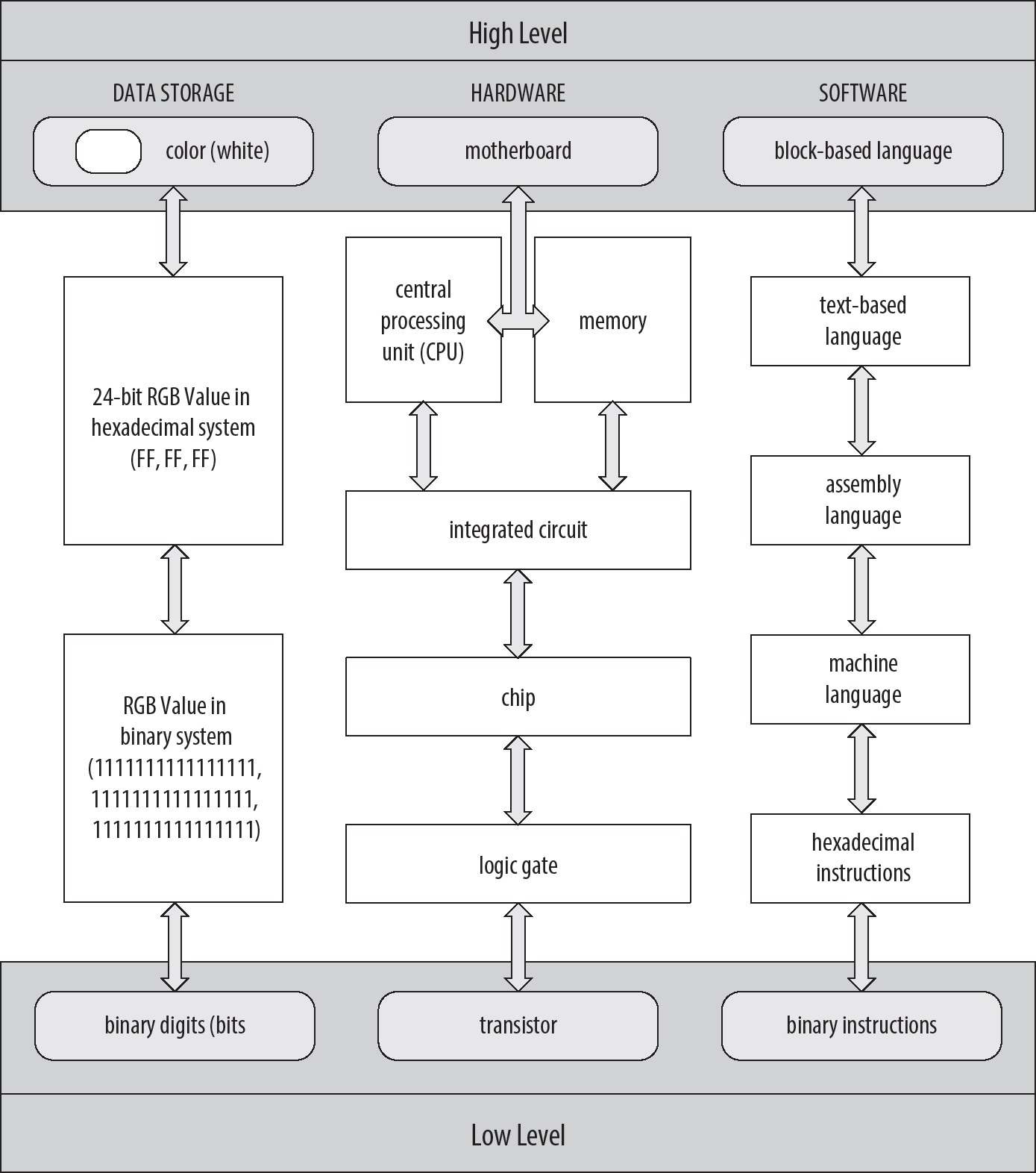
计算机系统从 "高层(High Level)" 到 "底层(Low Level)" 的三层(数据存储、硬件、软件)分层结构,核心是呈现 "抽象概念如何转化为底层实现":
1. 数据存储层(左侧)
从高层的 "直观概念" 逐步拆解为底层的二进制位:
- 高层:直接表示 "颜色(比如白色)"
- 向下转化:先变成 "24 位 RGB 十六进制值(如白色的 FF,FF,FF)"
- 再拆解:转化为 "RGB 二进制值(每色 8 位全 1,即 11111111)"
- 底层:最终对应 "二进制数字(bit,计算机最基础的存储单元)"
2. 硬件层(中间)
从高层的硬件组件,拆解为底层的电子元件:
- 高层:直接使用 "主板"
- 向下拆解:主板包含 "CPU(中央处理器)+ 内存",二者依赖 "集成电路"
- 再拆解:集成电路由 "芯片" 组成,芯片基于 "逻辑门"
- 底层:逻辑门的最小单元是 "晶体管"(计算机硬件的基础电子元件)
3. 软件层(右侧)
从高层的编程语言,转化为底层的二进制指令:
- 高层:用户使用 "图形化积木语言(如 Scratch)"
- 向下编译/解释:依次转化为 "文本编程语言(如 Python)" → "汇编语言" → "机器语言"
- 再编码:机器语言可简化为 "十六进制指令"
- 底层:最终对应 "二进制指令"(计算机能直接执行的代码)
低级语言与高级语言
先明确概念:低级语言更接近计算机底层(易被硬件执行,难写),高级语言更接近人类逻辑(易写,需编译/解释)。
一、常见低级语言
机器语言
计算机能直接执行的二进制指令(0/1 组成),完全依赖硬件架构,可读性极差。
汇编语言
机器语言的 "符号化版本"(用助记符代替二进制,如 MOV 表示 "移动数据"),仍依赖硬件架构,比机器语言易读,但仍需懂硬件知识。
二、常见高级语言
按用途分类:
- 通用开发:Python、Java、C++、JavaScript、C#
- 脚本/轻量开发:PHP(Web)、Ruby、Shell(脚本)
- 功能型/专业场景:Go(后端/云原生)、R(数据分析)、Swift(iOS 开发)、Kotlin(Android 开发)
核心区别:低级语言 "贴近计算机",高级语言 "贴近人类思维"。
COBOL 语言简介
COBOL 是一种什么语言?
COBOL(Common Business-Oriented Language,面向商业的通用语言)是一种高级编程语言,主要用于商业、金融和行政管理领域的大规模数据处理任务。
核心特点
诞生早:1959 年推出,是最早的高级语言之一,至今仍在银行、保险等行业的核心系统中广泛使用(比如处理海量账单、财务报表)
可读性强:语法接近英语,易于业务人员理解
稳定性高:设计初衷是 "业务逻辑长期不变",因此代码结构严谨,能支撑数十年的系统运行(许多 legacy 系统至今依赖 COBOL)
什么是逻辑门?
定义
逻辑门是物理硬件。
它是由晶体管、电阻、电容等电子元件在芯片上物理实现的电路模块。例如,一个简单的与门可以通过若干晶体管的导通/截止组合,来对输入的电信号(对应二进制的 0 和 1)执行 "与" 逻辑运算,并输出物理电信号形式的结果。
从计算机硬件的层级来看,逻辑门是构建芯片、集成电路的基础物理单元,是 "硬件世界" 里实现逻辑运算的实体组件。
工作原理
逻辑门是数字电路的基本构建块,它基于布尔代数,通过对输入的二进制信号(0 或 1,可理解为 "低电平/高电平" 或 "假/真")进行逻辑运算,输出一个二进制结果。
常见的逻辑门
与门(AND Gate):所有输入为 1 时,输出才为 1;只要有一个输入为 0,输出就为 0
或门(OR Gate):只要有一个输入为 1,输出就为 1;所有输入为 0 时,输出才为 0
非门(NOT Gate,又称反相器):输入为 1 时输出 0,输入为 0 时输出 1,实现逻辑取反
与非门(NAND Gate):是 "与门输出再取非",只要有一个输入为 0,输出就为 1;所有输入为 1 时,输出才为 0
或非门(NOR Gate):是 "或门输出再取非",所有输入为 0 时,输出才为 1;只要有一个输入为 1,输出就为 0
异或门(XOR Gate):输入不同时输出 1,输入相同时输出 0
重要性
这些逻辑门是构成计算机芯片、处理器等硬件的基础,复杂的计算和控制逻辑都是由它们组合而成的。
布尔函数和逻辑门的关系
布尔函数和逻辑门是 "抽象逻辑" 与 "物理实现" 的对应关系,前者是数学层面的逻辑描述,后者是硬件层面的实体实现。
具体关系
1. 布尔函数是逻辑门的 "数学定义"
布尔函数是基于布尔代数(0 和 1 为变量,通过与、或、非等运算组合)的函数,描述 "输入与输出的逻辑关系"。例如:
- 布尔函数
f(a,b) = a AND b描述 "只有 a 和 b 都为 1 时,输出才为 1" - 布尔函数
f(a) = NOT a描述 "输入为 1 时输出 0,输入为 0 时输出 1"
2. 逻辑门是布尔函数的 "物理实现"
逻辑门通过晶体管等电子元件组成的电路,将布尔函数的抽象逻辑转化为可执行的物理操作。例如:
- "与门" 对应并实现了
a AND b这个布尔函数 - "非门" 对应并实现了
NOT a这个布尔函数
3. 复杂逻辑的组合关系
复杂的布尔函数(如包含多个变量和运算的逻辑)可以通过多个基础逻辑门(与、或、非等)的组合来实现。例如:
- 布尔函数
f(a,b) = (a OR b) AND NOT (a AND b)对应 "异或逻辑" - 可通过 "或门 + 与门 + 非门" 的组合电路实现
总结
简单说:布尔函数是 "逻辑规则",逻辑门是 "执行这个规则的硬件工具",二者一一对应,共同构成了数字电路的逻辑基础。
模拟(Simulation)
什么是模拟?
模拟(Simulation) 是基于抽象概念对现实世界系统或过程进行计算机建模和重现的过程。它通过提取现实系统的关键特征和规则,忽略不必要的细节,在计算机中创建一个简化的、可控制的模型来模拟真实情况。
模拟基于抽象概念的理解
模拟本质上是一种抽象的应用:
- 提取关键特征:从复杂的现实系统中抽象出最重要的变量、规则和关系
- 简化复杂性:忽略次要细节,只保留对模拟目标有意义的要素
- 建立模型:用数学公式、算法或数据结构来表示抽象后的系统
- 执行模拟:在计算机中运行模型,观察系统行为
举例说明
1. 天气模拟
抽象过程:
- 提取关键变量:温度、湿度、气压、风速、云量等
- 忽略细节:单个分子的运动、微观湍流等
- 建立模型:使用物理方程(如热力学、流体力学)描述大气运动
模拟实现:
- 将地球大气层抽象为网格点
- 每个网格点存储温度、压力等数据
- 通过数值计算预测天气变化
2. 交通流量模拟
抽象过程:
- 提取关键要素:车辆数量、道路容量、信号灯周期、车速等
- 忽略细节:司机的个人驾驶习惯、车辆品牌等
- 建立模型:使用概率分布和规则描述车辆行为
模拟实现:
- 将道路网络抽象为节点和边
- 车辆抽象为移动的实体
- 模拟不同时段、不同路况下的交通流量
3. 游戏物理引擎
抽象过程:
- 提取物理规律:重力、碰撞、摩擦力等
- 简化计算:使用简化的物理公式而非完整的物理方程
- 建立模型:用数值积分方法模拟物体运动
模拟实现:
- 物体抽象为具有位置、速度、质量的点或形状
- 碰撞检测使用简化的几何算法
- 实时计算物体运动轨迹
4. 流行病传播模拟
抽象过程:
- 提取关键因素:人口密度、接触率、感染率、康复率等
- 忽略细节:个体的具体行为、社会关系网络细节等
- 建立模型:使用微分方程或随机模型描述传播过程
模拟实现:
- 人群抽象为不同状态的个体(易感、感染、康复)
- 通过概率模型模拟疾病传播
- 预测不同防控措施的效果
模拟的特点
1. 基于抽象简化
- 只保留对模拟目标有意义的特征
- 忽略不必要的细节,提高计算效率
- 抽象程度取决于模拟的精度需求
2. 可重复性
- 相同的初始条件和参数会产生相同的结果
- 可以多次运行模拟,观察不同场景
- 便于验证和调试模型
3. 可控制变量
- 可以独立改变某个变量,观察其对系统的影响
- 在现实中难以实现的实验,可以在模拟中轻松完成
- 支持"如果...会怎样"的场景分析
4. 成本效益
- 避免在现实中进行昂贵或危险的实验
- 可以快速测试多种方案
- 降低试错成本
5. 时间压缩或扩展
- 可以加速模拟(如模拟数年的天气变化)
- 可以慢速模拟(如观察快速化学反应)
- 可以暂停、回放,便于分析
6. 理想化条件
- 可以创建现实中不存在的理想条件
- 可以隔离单个因素的影响
- 便于理解系统的基本规律
模拟的局限性
- 抽象带来的误差:简化的模型可能无法完全反映现实复杂性
- 模型假设:模型的准确性依赖于假设的正确性
- 计算资源限制:高精度模拟需要大量计算资源
- 验证困难:某些模拟结果难以在现实中验证
总结
模拟是抽象概念在计算机科学中的典型应用。通过抽象,我们将复杂的现实系统简化为可计算的模型,在计算机中重现和预测系统行为。模拟让我们能够以低成本、高效率的方式探索和理解复杂系统,是科学研究、工程设计、决策支持等领域的重要工具。
